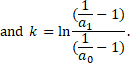Algebra of Measure (2)

We follow Euclid here,
except in the matter of parallels meeting.

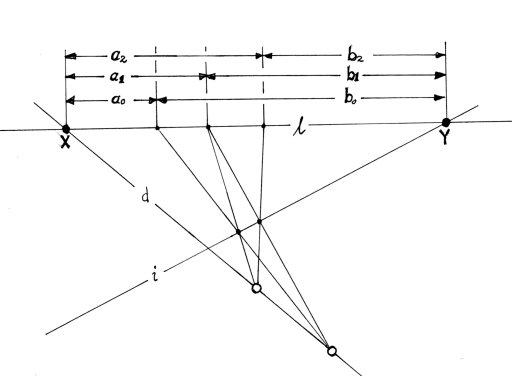
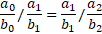
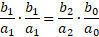
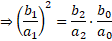
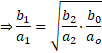
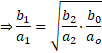
Growth Measure, based on Cross Ratio The method is similar to that used for the Geometric Progression. We have equal cross ratios, sharing end-points, X and Y — Rearranging, we obtain— from which we see that we have a geometric mean of ratios –	We sum an arithmetic series of logarithms with a common difference — Intermediate terms vanish, leaving — After some expansion and rearrangement, we reach our goal —