Some Formulae

Scans from the papers of Lawrence Edwards

Examples of the formulae in use

(Images © G. Calderwood; the mathematical content is public domain.)

An Artificial Example

Plot points A, B, C and D on a line

1. Calculate the positions of invariant points X and Y
2. Plot these positions on the line
3. Draw a line through X, and a line through Y
4. Select a point on the line through Y
5. Project plotted point B through the selected point on to the line through X
6. Project plotted point C through the selected point on to the line through X
7. These projected points are the directrices controlling the transformation
8. Use the directrices, and points B and C, to locate points A and D of the transformation

If the positions of points X and Y have been correctly calculated and plotted, Points A and D should fall, by pure construction, on their plotted positions.

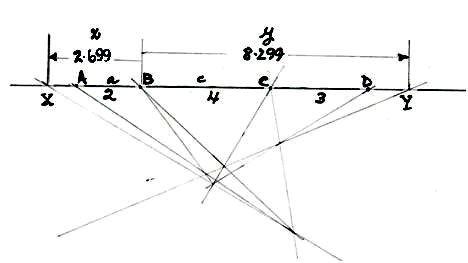
Given four points A, B, C & D on the line, and their spacings, we want the invariants, X & Y

a = AB = 2,
c = BC = 4,
d = CD = 3,
x = XB, y = BY.

We need the cross ratio, R, of the four points A, B, C & D to find the multiplier, m.





Now,


So,

These values are measured outwards from B, and tested by construction, above.  The agreement of construction with calculation is excellent.

A Natural Example

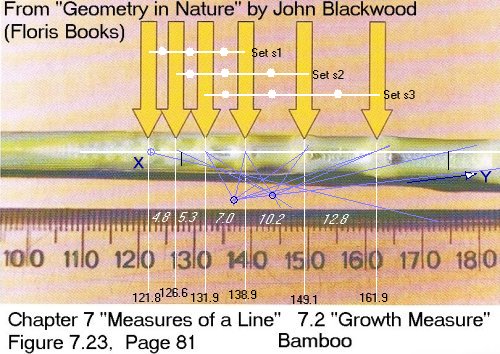
We use John's arrows and ruler to obtain three sets of three intervals (My markings)

Results

Set           a              c              d              R                 m                    Type
 s1           4.8           5.3           7.0         3.697        0.85+i0.51           circling
 s2           5.3           7.0         10.2         3.914        0.96+i0.28           circling
 s3           7.0         10.2         12.8         4.415           1.883                growth

We see that only the third set, s3, gives real invariants: the X invariant lies 16.86 mm (by John's ruler) left of the fourth arrow from the left.

Using the position of this invariant for the check-by-construction, we see that the positions of the nodes corresponding to s3 are accurately traced, but that other node-positions are not.

This suggests that we may have a measure that varies smoothly in "amplitude" along the length of the bamboo.

With thanks to John Blackwood.
His book, “Geometry in Nature”, is published by
Floris Books,
15, Harrison Gardens,
Edinburgh.
www.florisbooks.co.uk