Imagine that
we could take a line as we take a spurtle (in Scotland, this is about
ten or eleven inches of half-inch-diameter, wooden rod, usually with the effigy
of a thistle carved at one end, traditionally for stirring porridge)—and
use it to "stir space".
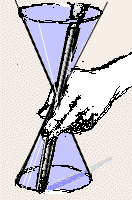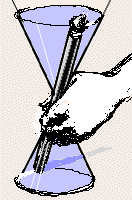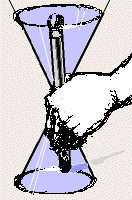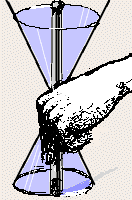
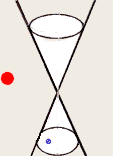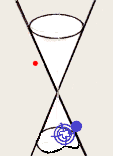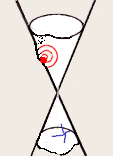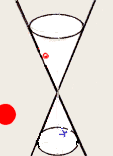
If we were to stir in such a way that a fixed point on the line would trace out a circle, then the line would sweep out a surface that is a right circular cone.
This cone has a vertex, equivalent to the place at which we grasp the spurtle. The line pivots in/on it.
I stress that this point does not divide the line (two would, but there is only one), so the vertex does not divide the cone. In the literature, one often sees it written that a cone consists of two parts, called "nappes", that meet in the vertex. This is mistaken. A cone must cut the plane at infinity as it passes through it. Just how that cut looks is a matter of great interest, and some controversy!
If we were to stir in such a way that a fixed point on the line would trace out a circle, then the line would sweep out a surface that is a right circular cone.
This cone has a vertex, equivalent to the place at which we grasp the spurtle. The line pivots in/on it.
I stress that this point does not divide the line (two would, but there is only one), so the vertex does not divide the cone. In the literature, one often sees it written that a cone consists of two parts, called "nappes", that meet in the vertex. This is mistaken. A cone must cut the plane at infinity as it passes through it. Just how that cut looks is a matter of great interest, and some controversy!