Home
Site Map
The Cone
Conics(2)
http://math2.org/math/algebra/conics.htm
http://mathworld.wolfram.com/ConicSection.html
There is another way to form Conics.
Conics (1)
There are Seven
Conics
(Conic Sections)
Made by Cutting a Cone with a Plane
|

|
 Circle
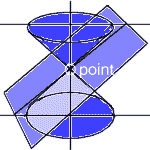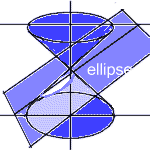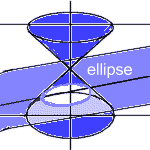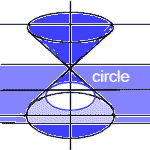
CircleEllipse Point Line-Pair Hyperbola Parabola Line |
The first thing to note is that
there is no way for a cutting plane
to avoid cutting the cone,
so a conic of some kind is inevitable,
but
- if the cutting plane's attitude with respect to the cone is
such then the conic must be a
 parabola,
(plane misses the vertex, and
lies parallel to a line of the cone.) hyperbola, (plane misses the vertex, and does not lie parallel to a line of the cone.) line-pair, (plane cuts the vertex, and does not lie parallel to a line of the cone.) line. ( plane cuts the vertex, and lies parallel to, and in, a line of the cone.) |
- if the cutting plane's attitude with respect to the cone
is such then the conic must be
a circle,
(the plane misses the vertex, and is at right angles
to the axis.) |
|
|
|
| The interactive diagram above left illustrates a cone cut by two planes in two conics, 'blue' and 'red'. The yellow line is common to these cutting planes. There is no absolute requirement to think of this line as being the "horizon", or at infinity, but one can, and if one does, then the two planes, and the two conics on them, will be parallel to each other. If in this case the cone's axis is taken to be at right angles to the planes, then, appearances notwithstanding, both conics must be circles, and the axis must pass through their centres.
The diagram on the right allows the vertex of the cone to be placed at the infinite, which yields a cylinder—and this tells us that a cylinder is a special case of cone! Drag the dashed blue line, g, around point G to move the vertex on the cone's axis, a. To have the vertex at the infinite, make line g lie parallel with the cone's axis, a. |