Geometric Inidentity
(page under development)
Since geometric intervals do not have size,
they can neither be equal nor unequal.
However, they may be identical, or inidentical,
by way of elementary incidence.
Geometric intervals that do not project each into the other are inidentical
Degenerate and Non-degenerate Conics
A conic may be defined by five points in the plane.If any three of the five are co-linear,
the conic degenerates into a pair of lines.
To see this degeneration in action,
drag any three of the five ‘points’ below into line.
drag any three of the five ‘points’ below into line.
Projective
Comparison of Intervals on a Line
via a Degenerate Conic
Projective
Comparison of Intervals on a Line
via a Non-degenerate Conic
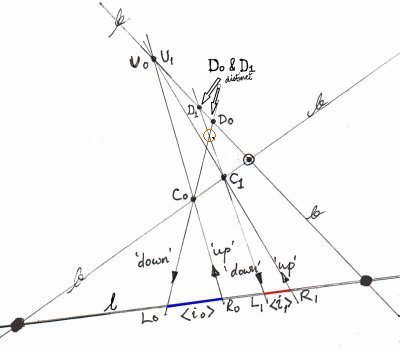
The end-points L0 and R0 of the blue interval i0 on line l are projected via some intermediate point C0 on the conic C by lines d0 and u0 respectively into directrices D0 and U0 respectively, which are also on the conic.
The same procedure is followed for the red interval i1,
except that line u1 is chosen to project R1 into point U1 such that directrix U1 is coincident with directrix U0.
Line u1 also defines the intermediate point C1 on the conic C.
Line d1 then projects end-point L1 via intermediate point C1 into directrix D1 on the conic C.
If directrices D0 and D1 do not coincide, the blue and red intervals are geometrically in-identical.
Else, they are identical.
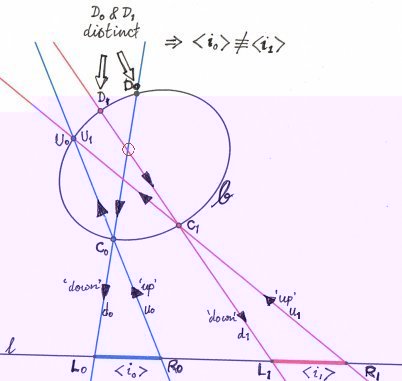
The end-points L0 and R0 of the blue interval i0 on line l are projected via some intermediate point C0 on the conic C by lines d0 and u0 respectively into directrices D0 and U0 respectively, which are also on the conic.
The same procedure is followed for the red interval i1,
except that line u1 is chosen to project end-point R1 into directrix U1 so that U1 is coincident with directrix U0.
Line u1 also defines the intermediate point C1 on the conic C.
Line d1 then projects end-point L1 via intermediate point C1 into directrix D1 on the conic C.
If directrices D0 and D1 do not coincide, then the blue and red intervals are geometrically in-identical.
Else, they are identical.
You will see that the wording above is the same for both conics.
This is because they are, from a strictly geometric vantage, indistinguishable.
Do please note that the line, l, can, but need not, cut the non-degenerate conic,
but the line, l, must cut the degenerate conic.
In the degenerate case, the line must always cut the conic in two real points, but in the non-degenerate case, it can cut the conic in either two imaginary points, or in two real points.
Recovery of Identity
However, in both the degenerate and non-degenerate cases,
inidentical intervals
may be made identical once more, by using the conic
that
passes through the meeting-point (shown ringed in orange above)
of the “down” lines,
L0D0 and L1D1
to carry the directrices Un and Dn
—
which effectively brings points D0 and D1 precisely together.
Constraint on Recovery (to develop and illustrate)
Thus it is in principle always possible to find projective circumstances
that will compel two, randomly-made, distinct intervals of the same line to be identical,
but by the same token it is clearly not always possible to find projective circumstances
that will compel three or more such randomly-made intervals to be identical.
Projective Frame (to develop and illustrate)
Since, as noted above, the conic, whether or not it is degenerate, cuts the line l in two invariant points,
an action which compels a pair of priorly inidentical intervals on a line to be identical is
equivalent to redefinition of the projective frame of reference
in which the intervals may be compared.
But we must keep constantly and keenly in mind that,
since equality and calibration play no rôles here,
the comparison is not one of size or magnitude.