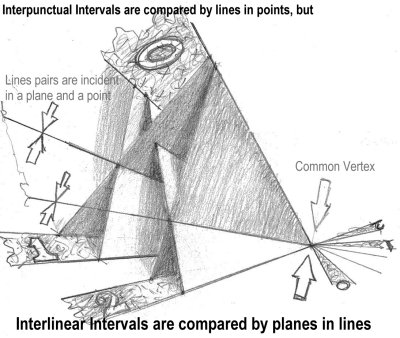
Interlinear Intervals
Interval 1 is equivalent to interval 0, and interval 2 is equivalent to interval
0, each by elementary incidence of two planes through a single, common line
(arrowed on the left, above), so that interval 1 is equivalent to interval 2.
Note that intervals 1 and 2 can be, but need not be, coplanar. However,
all the planes involved must be incident in the same point – the "common vertex"
indicated above. Else the comparisons will not work. |
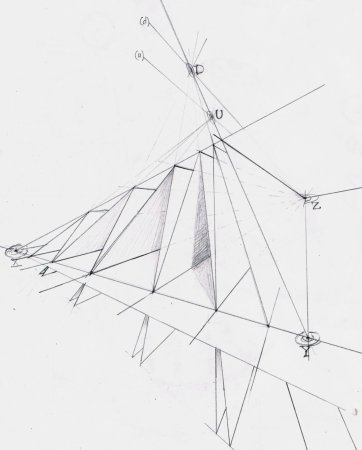
An interlinear protractor, similarly to an
interpunctual ruler, is devised by iterative replication of equivalent,
interlinear intervals, on a single plane, via perspectivity and projectivity, as sketched
below. Like the interpunctual ruler (which “terminates” twice, in
so-called invariant points), this iteration also “terminates” twice,
but
in so-called invariant lines, XZ and YZ, so this style of protractor cannot deal with continual rotation,
which does not terminate.
|
The animation below illustrates the
iterative construction of a projective protractor.
You may control the animation using the buttons below it.
The apparent effect is to rotate the red line on the pale blue plane in discrete steps around the point Z,
but, strictly speaking, we see only the sequential steps of a
construction, not an actual movement of anything geometric.
We see that the protractor can be made simply by making the
lines in the pencil incident with the points of an interpunctual ruler
in the same plane.. |