←Tutorial page                  ← Comparison 10: Continuity and the Fundamental Theorem                  ← Comparison(11) - That Curve!

Strictly-Projective Motion of an Element
re transformation - page(s) under development.  Deeply relevant to physics!

(1) Motion of a Point in a Line
(Translation)

If we wish to move a point along a line strictly projectively, which is to say by elementary incidence alone, two, successive, ‘instantaneous’ positions of that point must form an interpunctual interval on the line — and then, three, successive such positions must form two, contiguous, interpunctual intervals on the line.

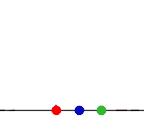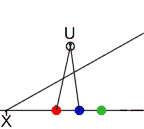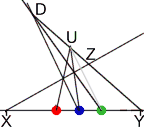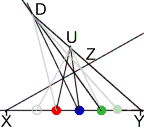Given three, successive end-points of two, contiguous intervals, and a “terminator”, the corresponding projective ruler can be found.

The stages of motion must therefore be successive end-points of the intervals of the projective ruler, and the projective motion of the point must consist of the translation from one end-point to the next.



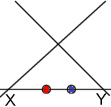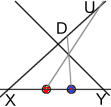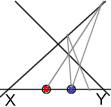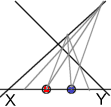
Please note carefully that the interval end-points are the only positions available to the projectively moving point, and that the moving point and the end-point are one and the same thing.


So the translation between end points of intervals —
  • must be stepped
  • and instantaneous.
 A projectively-moved point cannot slide on a line
 like a bead on a string, as here,
because the positions are necessarily discrete - that is to say, distinct, and non-continuous.

Accordingly, if the projective motion of the point is to be constant and uniform, and expressed as some constant number, say v, of intervals per constant, successive interval of time (we might call v the ‘projective velocity’ of the moving point), then the interpunctual intervals must be projectively identical, and v must be an integer.

Incidentally ...

Projectively, a point is a place, a somewhere, and nothing else at all: we therefore here seem to consider how a place may be moved from place to place.  This is at least paradoxical, and raises obvious questions.

Among them -
  • Under which circumstances can some places be mobile and others not?
  • Can two or more places be in the same place?
  • Can one place be in two or more places?

The places in question are, however, specified by elementary incidence — in this case, of lines, because the incidence of two lines, if it exists, is a place, on a plane.

(2) Motion of a Line in a Point
(Rotation)

(3) Motion of a Plane on a Line
(tentatively - ‘Swing’)

We work with interplanar intervals, here – those treated as “dihedral angles” in the Euclideo-Newtonian domain.  Now, angle does not work for pure projective geometry, because
  1. it denotes an interval between lines in a point, not between planes in a line, and
  2. specifies a size as a sum of absolute, equal sub-intervals (units), and
  3. dihedral angle in particular needs absolute, right angles to exist.
The requirements in items 2 and 3 are simply unavailable to pure projective geometry.

We therefore need a word to capture what happens when a plane moves. ‘Rotation’ relates to lines, not planes. “Swing” is offered.

(4) Translation of a Point, P, in a Line, p, as
that Line Rotates in that Point and in a Plane, π
(tentatively - ‘Slew’)

Here, a basic question arises concerning relativity, as we are having to deal with two motions at once: two elements of the three (the point and the line) are mobile (for the moment, we take the plane to be fixed).