- assumes that an interval has an absolute size,
- assumes that two or more intervals can be of equal size [video],
- and, using sums of equal ‘units’, tacitly conflates number with geometry.
Projective Geometry and Euclid part company here, because there is no exclusively geometric way to validate these assumptions, meaning that,
for
Projective Geometry, size and equality do not exist,
and, in direct consequence,
it can compare
intervals only through incidence.
Intervals
are matched – or mismatched –
by incidence alone.
A List of Consequences :-
-
An interval is
always the incidence of no fewer than three
geometric elements (see sketch on the right).
- Because an element is not three things, but just one thing (namely, itself),
- and an interval is three things (elements), not one thing,
-
an element cannot be an interval,
- and an interval cannot be an element.
-
Because, from (2) above,
- no geometric element is an interval,
- and because sizes are intervals,
Lines haven't length (not even ∞):
Planes haven't area (not even ∞2).
As there are three elements – point, line and plane – there are three fundamental types of interval ...
- Interpunctual - between two points incident with a line
- Interlinear - between two lines incident in a point and a plane
- Interplanar - between two planes incident in a line
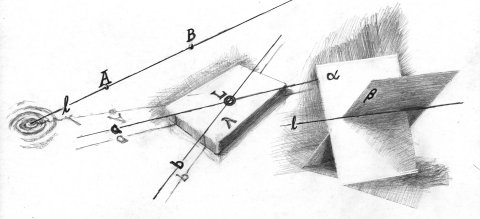
We note in passing that, for every type, whenever one interval is formed, two are in fact formed.
For example, we may trace out one interval going right from
A
to B on the line l, shown on the left above,
and may also trace out a second interval going left
from A to B. (The latter tracing works
because a line has no ends.) This fact is of significance when
investigating the validity of infinitesimals for non-Euclidean, projective
geometry.
Intervals have ends, Elements do not.