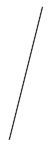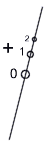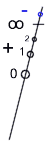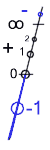Home      Site Map

 

On Flags and Numbers

I hope the seasoned mathematician, or anyone to whom the following is known or obvious,
will forgive me for labouring the topic, but I believe many find it vexed,
and there are one or two fundamental issues embedded subtly
within it that even the most seasoned may wish to revisit.


Natural Counting

Natural counting

 

 

 

We are naturally inclined to assign numbers to intervals on a line as we make them, or as they are made–we simply count them as we go. We usually assign the counts to the points marking the intervals, rather than to the intervals themselves, with the tacit understanding that the 'n' of the n'th point in a range also refers to  the interval between that point and the "one before"–the (n-1)'th point.

N.B. - Because we are working with
strict projective geometry,
which preserves elementary incidence alone,
and can neither support nor detect equality,
we are here merely counting intervals as items,
NOT summing them to a size.
Where to Start?


However, since the range extends indefinitely on the line in either sense from any point, any point in the range can be labeled '0' (zero), with the simple meaning, "We will start counting here!" We can do this because points are without size, so we have as many places available for counting as we wish, going in either sense from any start. We surely won't run out of them.

Which way?

But it is obvious that we will have a problem with knowing, just from the numbers themselves, in which sense we are counting points, because the numbers are the same either way.

In what follows, please bear firmly in mind that
a point is not a line,
and
a line is not a point,
and that, though either may be incident with the other,
neither consists of the other.

Given a sequence on a line
there is no guarantee that the first and final end-points
of a number of its intervals
will match
two distinct, randomly-selected places.
on that line.

Continually subdividing the intervals need not lead to a fit of a whole number of intervals between our points, because their positions were not selected by the sequence.

In fact, the only sub-division projectively available (that is, found by using a straight-edge alone) is, ‘by two’ – bisection. After this, by serial, repeated division-by-two of such sub-divisions, division by powers of two –

20=1, 21=2, 22=4, 23=8, 24=16, 25=32, .......

– becomes possible, and, clearly,

only points falling exactly at such subdivisions
can be noted and counted by the numbering system built on these subdivisions
(that is, by this “calibration” ).

All other points in the line must simply go undetected. Such points must be unfittable and uncountable—and hence, unmeasurable.

 divby2

On the other hand,
Given the points
(and the invariants), it will always be possible to find a sequence with intervals that do fit. By conscious construction, we take the interval between the two, given points as an interval of the sequence.

We can extend this to one given invariant, and a maximum of three randomly-selected points. The position of the second invariant is determined by the selection of these first three points, and this in turn determines the position of the fourth point, and indeed the positions of all other points in the sequence. This is an expression of the Fundamental Theorem.


A randomly-selected fourth point could be, but need not be, in the appointed fourth position.

If we insist that an unfittable point must have a number (which, as we perhaps now see, may not be an altogether wise thing to do), then we must accept that that number is not determined by the given sequence.
Flags (Signs)

With all the above clearly in our minds, we can say points-cum-intervals in the sequence "before", or, "to the left of", zero should carry a little flag (conventionally, '-') indicating that, "we are counting up, but backwards/leftwards", or, "we are lying to the left of zero".

flags

We could just as well put these flags on the intervals, "counting up, rightwards/forwards", or, "lying to the right of zero".  It doesn't much matter where they go, provided we remember that they are just there to keep us in agreement about where we are and what we're doing,
and stick to our decisions about how to use them.

The animation shows "+" flags on the numbers running right from zero. These are very often simply omitted, as they are supposed to be "tacit", or "understood", meaning, 'if a plus sign is not there, the number is positive.'

This is sometimes unhelpful, as zero and infinity are always unsigned. Moreover, occasionally we want to refer only to the value of a signed number (the so-called "absolute" value, e.g., |x|). The confusion is compounded by statements like, "Absolute values are always positive", which is simply untrue: they are neither positive nor negative.

We also need flags because, as we have seen, we are assigning the same numbers twice, in two different senses.

The issue of flagging and numbering is a source of enormous and endless confusion, especially in classrooms, in which it may for instance be heard that, 'quantities can be less than nothing', which is nonsense, or that, 'minus times minus is plus', which seems like nonsense.

If we say,
"lying to the left or right of"
 we are speaking  positionally.
We are specifying where something is - passively.
Passive Flags

On the other hand,
if we say,
"going rightwards/leftwards,
or,
forwards/backwards",
we are speaking operationally.
We are doing something - actively.

Active Flags

So our flags are also used twice, like the numbers: they can be both passive signs and active operators.

So, for example, when we multiply, we operate, and when, operating, we multiply minus by minus, we are simply issuing the command, "Reverse!  Go the other way round!  Stop what you're doing, and do the opposite!"  We were "going left", or whatever the second minus meant, before, so on multiplying by the first minus, we will be "going right", or positively, after.  Minus times a minus is a plus.  So simple, so easy to forget!

By this flagging scheme, neither zero nor infinity carries a flag--both are unsigned.
Both mark a place where transition may be made from the section with one sign to the section with the other. Indeed, their roles may be swapped.  If we are to leave "plus territory" and enter "minus territory", or vice versa, we may do so only by way of one of these two places (this serves as a reminder that one point does not divide a line; two do).

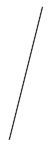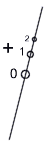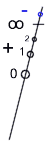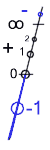Please do notice also that the numbers, as quantities,
are always either zero, or more than zero, never less. They simply cannot be less.

Mention has been made here only of lineal sequence
- intervals of stepping from point to point along a "fixed" line. -
Nothing is said about angular sequence
- intervals of rotation of a line around a "fixed" point. -
These ideas are dual.
We will find that the two kinds of sequence are dual, too.

Home      Site Map