←Tutorial page                  ← Related page                  ← Comparison 9 - Skew rulers                  Comparison 10 - Interlinear intervals →                  The Tetrahedral Complex

Discussions

(1) Swept Surfaces: a Euclidean cuckoo-in-the-PG-nest?

Consider this, from the marvellous Wolfram: MathWorld.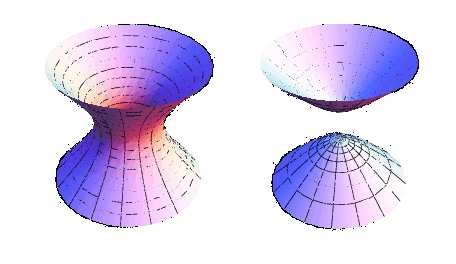



The article describes the hyperboloid as “a surface of revolution.”  It is a fine example of a so-called “swept surface”, made - somehow - by a plane curve swung bodily around an axis in the curve's plane. The ‘somehow’ is not discussed.

 Such surfaces are disallowed by pure projective geometry, 
 as there is no projective way to move (transform) an 
 entire, intact curve in the requisite fashion — 

— let alone a way to have it leave a trace (a ‘locus’), that somehow ‘builds’ the surface.  In particular, in this instance, we see  the notion of preserved (constant) radii deployed – perhaps instinctively, or from habit.

Now this is a purely Euclidean notion, as size, whether or not constant, is not preserved under projective transformation, so constant radii are simply unavailable.

In consequence, we must conclude for the same reason (viz, that size is not preserved), that the structure of skew lines between our skew rulers cannot be a swept surface.

Moreover, the hyperboloid structure (which is actually built of non-incident skew lines), cannot be a continuous surface.  In fact, it cannot be a surface at all. See the panel on the right.

This cannot become a continuous surface,

because it is a structure of skews, with each
forever entirely out of touch with every other,
no matter how many there are!

To form a continuous surface, the skews would need
to join up, add (integrate), merge, connect, in some way.

But that is just what skews, by definition, cannot do.

So for this reason alone, they cannot, ‘in the limit’, be joined in the way of the integral calculus – that is, by infinite crowding – but also because, without size and equality, they cannot even detect, recognise or evaluate this infinite - or, indeed, infinitesimals.

[Should the lines come actually to touch (to be incident), they would not then be skew, and could lie in a 'continuous' surface.  But that surface could not be a hyperboloid.  It might be a cone.]


The discontinuity (‘disincidence’, perhaps?) necessarily inherent in these structures is a matter of great importance, especially in regard to their coherence – which cannot be due to rigidity (the preservation of constant distances), as we have just seen.  Can we speak of a degree of disincidence, and avoid contradiction?

While the structure illustrated above cannot form a surface (so long as it is not degenerate), it is not disordered.  In fact it forms what I call a “tetrahedral complex”, which is a net, or mesh, of tetrahedral "cells" — which is considerably more interesting than a mere surface.