Five Planes, and Desargues
A note: Though I would ordinarily deprecate doing so, here, simply for convenience, I use the word, "common", for an element that is the incidence of two elements. The word can be quite wrongly construed to mean that the element-of-incidence is part of both incident elements, which it never is, because elements do not have parts.
Especially note that the planes of 3-p have a common point, O, and collectively, three common lines, and the planes of 2-p have a line in common.
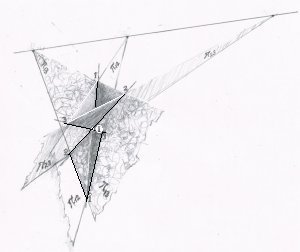
The whole assembly is a “prismatic cone” - or a “conical prism” - having two, triangular cross-sections, made by the two planes (not depicted on the left) of group 2-p — their line in common is the one drawn across the top of the sketch.
The 3-p planes -
- form the “walls”,
- their three common lines the “corners”,
- and their common point the vertex, O,
The drawings are given as an aid to the imagination – and in the hope of making clear that the Desargues Configuration [*], which this is, is
the complete incidence of five planes.
Another view of the Five Planes -
.jpg)
This always happens when and where five planes congregate.