The Detection of Absolutes (2)
in which we try by experiment to test an hypothesis ...
Recap
It is shown here that neither translational nor rotational measure can be had from elementary geometry, and that in fact no kind of measure can be had.So, acting on the very common supposition that Nature and Geometry bind seamlessly to each other, we may turn to Nature to see how She copes.
In Nature, we observe perspective, which entails special, so-called “ideal”, points at infinity – the points in which certain co-planar lines, which are ‘special’ by way of being parallel, appear to meet.
But ‘special’ qualites are adventitious and extraneous, because
- all points are ordinary points (a point has exactly one quality, not two or several, so cannot have ‘special’ as a quality as well as place)
- non-skew, co-planar lines always meet and so always have a point in common, so parallelity, if it exists at all, is not a geometric property
This specialisation grafts equality
on to projective intervals
to confer on them
an entirely non-native and quite extra-ordinary property
– namely, size.
It recasts
a simple count of sizeless intervals
as a sum of units.
on to projective intervals
to confer on them
an entirely non-native and quite extra-ordinary property
– namely, size.
It recasts
a simple count of sizeless intervals
as a sum of units.
The supposition is that
if the real invariants, X and Y, are both placed at ∞,
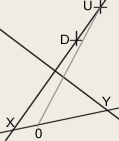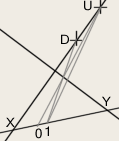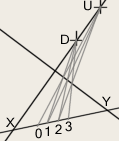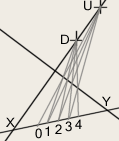
↑ a Simple Count of Sizeless Intervals ↑
↑ as illustrated above, ↑
is converted to
↓a “Sum of Equal Units”, ↓
↓ as illustrated below. ↓
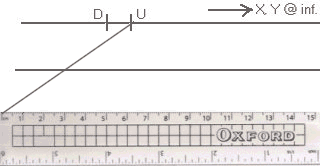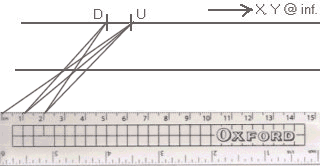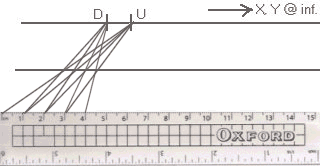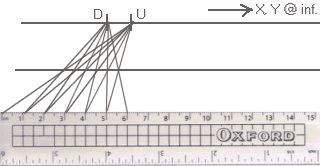
But this is wholly empirical, and the ‘supposition’ is an hypothesis that must be tested.
If ...
- Calibration and Size are so intimately and immediately linked to elements ‘at infinity’, and
- if Nature and Geometry bind seamlessly,
as is hypothesised here, and recapped on the left,
actually find (i.e., detect) these elements
in their natural places ...
... and establish their existence as
natural objects.[ * ]
natural objects.[ * ]
- The first photograph below,
of ‘lines’ ruled on paper,
should test our ability to do this.
There are among them
two differently-orientated pairs
of ruler-and-set-square-drawn parallels.
Find and mark these pairs.
We see that in order to locate the pairs of parallels, we would –
- have first to locate all of the meeting points of all of the lines, each with every other,
- then have next to determine which of these points lie in - or at - the photographic infinite, which is a unique line.
However, there is nothing in the photograph (which, do please note, is our sole and only source of objective information) that allows us to locate its infinity, so the attempt to locate the photographed parallels must always fail.
-
The second photograph is of conics.
Two of them are circles,
drawn with compasses.
The circles are there to represent
absolute isotropy on a plane.
Find and mark the circles.
We see that to find the embedded circles, we have, in addition to locating the photographic infinity, to find those conics for which the radii are constant, because every conic has a pole cum centre, corresponding to the line at infinity as its polar,
whether or not the conic is a circle.
The detection of circles requires more than detection of poles/centres.
The photograph offers nothing to help us do this, so attempts to locate circles must also always fail.
So,
because the absolute, natural infinite
defies detection,
the hypothesis is untestable.
we must conclude that
there is no geometric way to detect or establish
absolute, isotropic equality.