Home
Site Map
Path Curves (2)
Path Curves (3)
Path Curves (4)

Path Curves in the Plane (1)

We add a Dimension

Stepping a point along a line produces linear measures. This is One Dimensional, as it is confined to a line..

Next, we step a line (red) across a plane (blue), as we want to use two such stepping lines to track a point as it steps across a plane. That track must represent the combination of two linear measures. This is Two Dimensional, as it is confined to a plane.

 

Where for the steps on a line we used

  • two directing points in a line and an
  • intermediate line,

now, for the steps of a line on the plane, we use

  • two directing lines in a plane (yellow), and an
  • intermediate plane (dark blue).
  
We move a red line, first lifting it in a plane (gray) through one of the directing lines ('up', or u) until it encounters the intermediate plane, then returning it along another plane (pale gray) through the other directing line ('down', or d). All this can work only if the red line and the directing lines all pass through the meeting point of the three coloured planes.

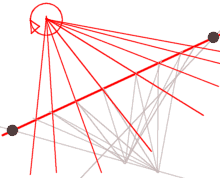
It is at once evident that stepping a line across the plane must always rotate that line in a point.

We have the dual of stepping on a line.

We would see the rotation arrested at the measure's end-points.

What sort of measure would let the rotation continue indefinitely?

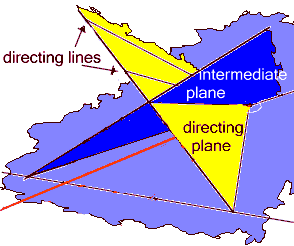
pcframe

pcframe pcframe pcframe

When all is done, we see that we can conveniently direct our stepping line in Z through the stepping point of a linear measure, and do not need to go through the fairly elaborate construction on the left—though we did need to do it at least once, to be quite sure of our principles!

Home      Site Map      Path Curves (2)      Path Curves (3)       Path Curves (4)