Home
Site Map

Path Curves (1)

Path Curves (3)

Path Curves (4)

Path Curves in the Plane (2)

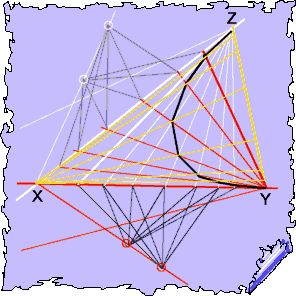
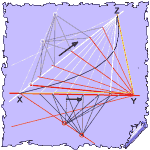
As we indicated we would, we next track a point stepping on the plane as the intersection of two stepping lines, as illustrated below right

—one red, rotating in point Y and guided by a linear measure in the bold white line, below, and —one white, rotating in point Z and guided by another, different linear measure in the bold red line, below. The bold white and red lines share point X, which is also an end-point of each of the two measures.

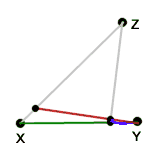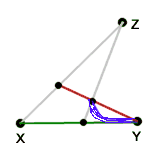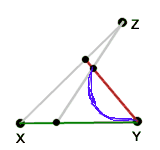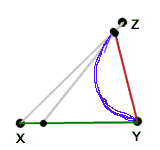The stepping point traces out an invariant path curve.

Notice that it passes from Y to Z and avoids X.

If we were to take another red/white pair, we would get
another path curve on a different route between the same vertices, but with
identically the same shape.

The λ of the curve above is the ratio of the characteristic multipliers of the two measures.

A yellow line through X and the stepping point steps along with it, and cuts the bold, yellow YZ line in a range of points—which as may be seen is a third linear measure.

Now XYZ is an "invariant triangle", so the stepping point is in fact guided by three measures, one in each side of this triangle.

In this construction, you place vertex C by clicking on and rotating the line through point T, and you can send C to ∞ by aligning the rotatable line with the faint blue line also through T and “parallel” with line AC.

Side AB can be set “at right angles” to side AC by aligning AB with the faint blue line through vertex A.