Formal Proof of Invariant Incidence
There is a risk of circularity here, as the Theorem of Desargues depends on perspectivities,
and in what follows, we have perspectivities depending on the Theorem of Desargues.
It is to resolve.
and in what follows, we have perspectivities depending on the Theorem of Desargues.
It is to resolve.
The two “intervertical” lines, p and m, incident in
G, are common to both pairs of Desargues triangles,
blue and red, so the pairs share a “perspector”, and a
“perspectrix”. A similar exercise undertaken with Δacb1 (ΔPMU) and
Δ1
(Δ) would lead to the same
point, G, so one may say that the incidences on which a
ruler depends are independent of particular constructions, provided they all
begin from the same four of the base points.
Formality aside, the ‘barred’ and ‘unbarred’ constructions are
‘shadows’ or perspectivities, of each other, from centre
G, so
‘mutually shadowed’ intervals
are equivalent or identical.
‘mutually shadowed’ intervals
are equivalent or identical.
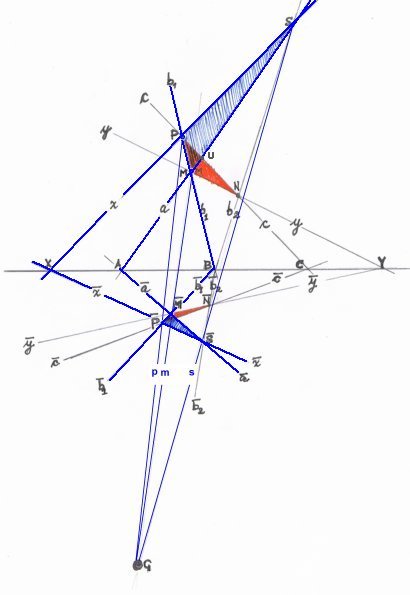
Because
- side x is incident with side in point X
- and side a is incident with side in point A
- and side b1 is incident with side 1 in point B
- and X, A and B are collinear,
Lines p, m and s, joining corresponding vertices, therefore converge in point G.
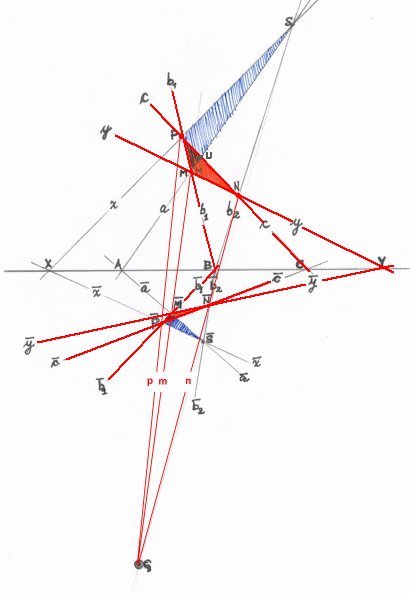Because
- side y is incident with side in point Y,
- and side c is incident with side in point C,
- and side b1 is incident with side 1 in point B,
- and Y, C and B are collinear,
Lines p, m and n, joining corresponding vertices, therefore converge in point G.