Replication
Can the same ruler be constructed from other elements?
On this page, we see a ruler created from two, contiguous intervals and one “terminator" — which is to say, from four, given points in the line. It is reproduced below.
If the ruler is to be and stay useful, we need to be sure that every possible construction on those first four, given points will lead to the same, fifth point, and to the same reference interval.
In fact, it is guaranteed, by the Theorem of Desargues[1] [2].
The red and blue constructions are on different planes, incident in the black line, and each is the other's “shadow”, from “source” P0 (the “perspector”). On the black line (the “perspectrix”), the shadows are merged (degenerate).
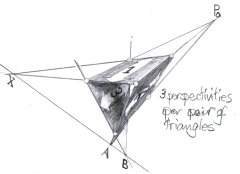So, we have several perspectivities in P0,
comparing several Desargues triangles, and
finding them equivalent.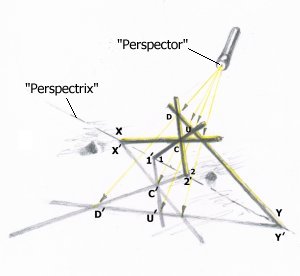
Merely by inspection, we see that the points on the perspectrix must stay exactly where they are, wherever the source goes, as these points and their shadows are the same things (try dragging P0!) – so their distribution must remain constant, too. Formally, they are invariant under central projection, and Desargues provides the formal proof of it.